Eclipses During 2031
By Fred Espenak
Based on the Article Published in
Observer's Handbook
2031
,
Royal Astronomical Society of Canada
In 2031, there are 2 solar eclipses and 3 lunar eclipses:
| Eclipses During 2031 | ||||
|
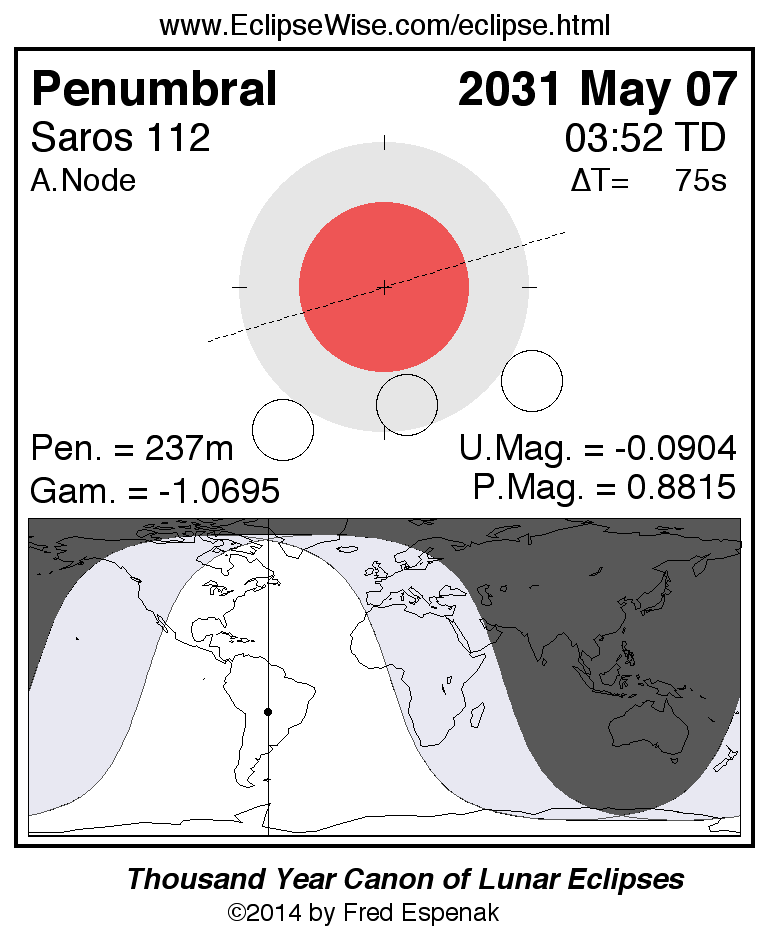
Penumbral Lunar Eclipse 2031 May 07 
|
Annular Solar Eclipse 2031 May 21 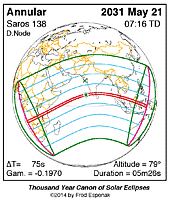
|
Penumbral Lunar Eclipse 2031 Jun 05 
|
Penumbral Lunar Eclipse 2031 Oct 30 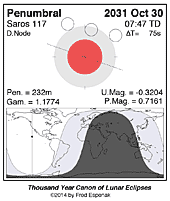
|
Hybrid Solar Eclipse 2031 Nov 14 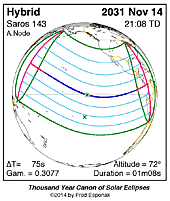
|
Unless otherwise stated, all times and dates used in this publication are in Universal Time or UT1 [1]. This astronomically derived time system is colloquially referred to as Greenwich Mean Time or GMT. To learn more about UT1 and how to convert UT1 to your own local time, see Time Zones and Universal Time.
Click for larger more detailed figure
Penumbral Lunar Eclipse of 2031 May 07
Under Construction
Diagram and map of the eclipse (Figure 1).
Table 1 lists predicted umbral immersion and emersion times for 25 well-defined lunar craters. The timing of craters is useful in determining the atmospheric enlargement of Earth's shadow (see Crater Timings During Lunar Eclipses).
This is the xx th eclipse of Saros [6] series 112
Complete details for the xx eclipses in the series may be found at Saros 112.
For more information about this eclipse, see the EclipseWise Prime Page at Penumbral Lunar Eclipse of 2031 May 07
Click for larger more detailed figure
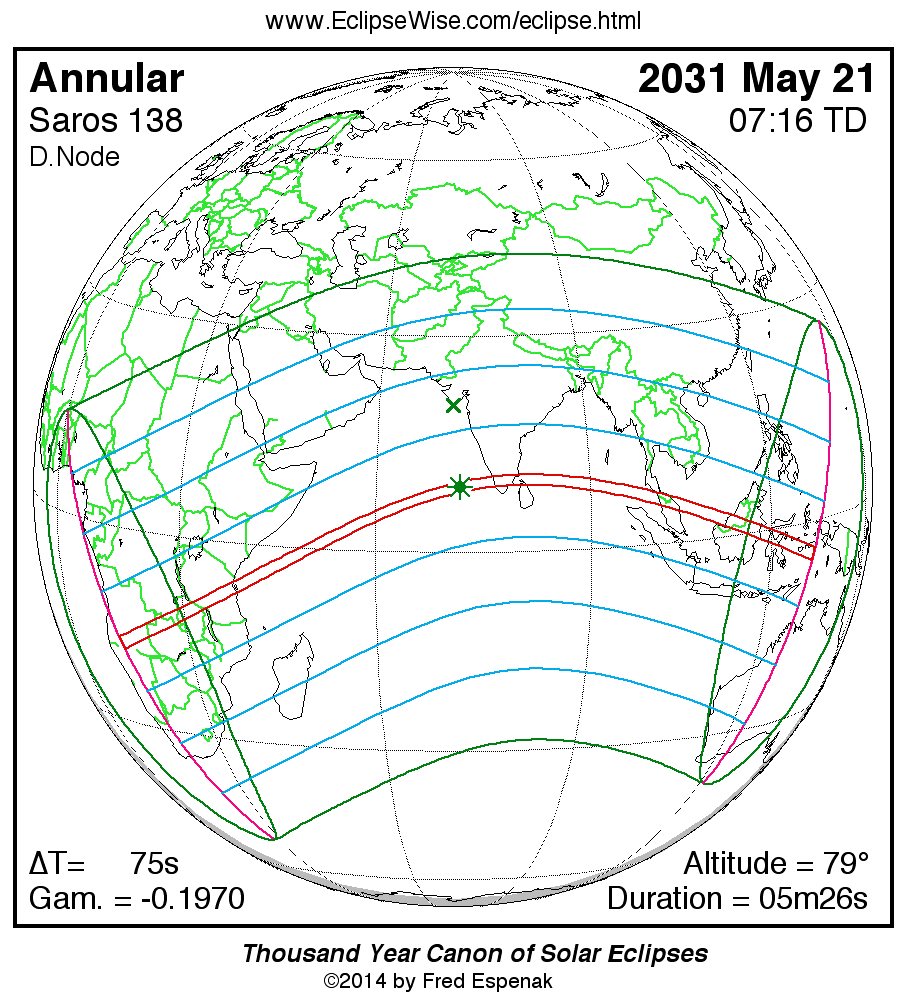
Annular Solar Eclipse of 2031 May 21
Under Construction
Map of the eclipse (Figure 2).
Local circumstances for a number of cities are given in Table 2.
The 2031 May 21 Solar Eclipse Circumstances Calculator is an interactive web page that can quickly calculate the local circumstances for the eclipse from any geographic location not included in the table.
The path of the eclipse is plotted on an interactive map at Google Map of the 2031 May 21 Solar Eclipse . This map permits zooming and scrolling as desired. Clicking the cursor on any location calculates the eclipse circumstances for that location. For more information see Key to Google Eclipse Maps.
This is the xx th eclipse of Saros [6] series 138.
Complete details for the xx eclipses in the series may be found at Saros 138.
For more information about this eclipse, see the EclipseWise Prime Page at Annular Solar Eclipse of 2031 May 21.
Click for larger more detailed figure
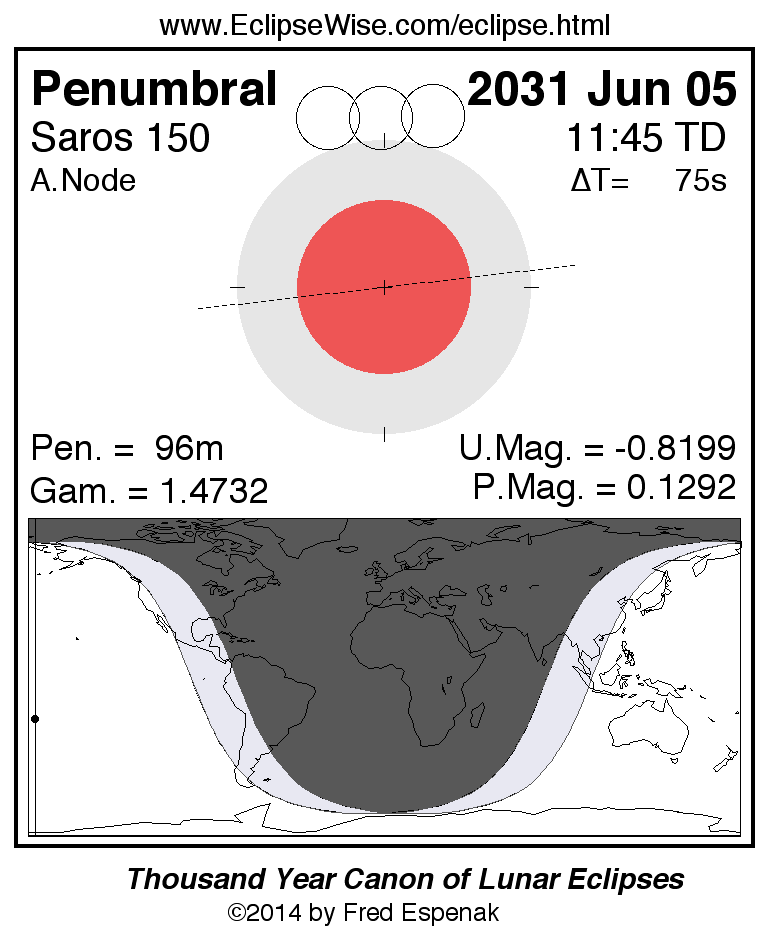
Penumbral Lunar Eclipse of 2031 Jun 05
Under Construction
Diagram and map of the eclipse (Figure 3).
Table 3 lists predicted umbral immersion and emersion times for 25 well-defined lunar craters. The timing of craters is useful in determining the atmospheric enlargement of Earth's shadow (see Crater Timings During Lunar Eclipses).
This is the xx th eclipse of Saros [6] series 150
Complete details for the xx eclipses in the series may be found at Saros 150.
For more information about this eclipse, see the EclipseWise Prime Page at Penumbral Lunar Eclipse of 2031 Jun 05
Click for larger more detailed figure
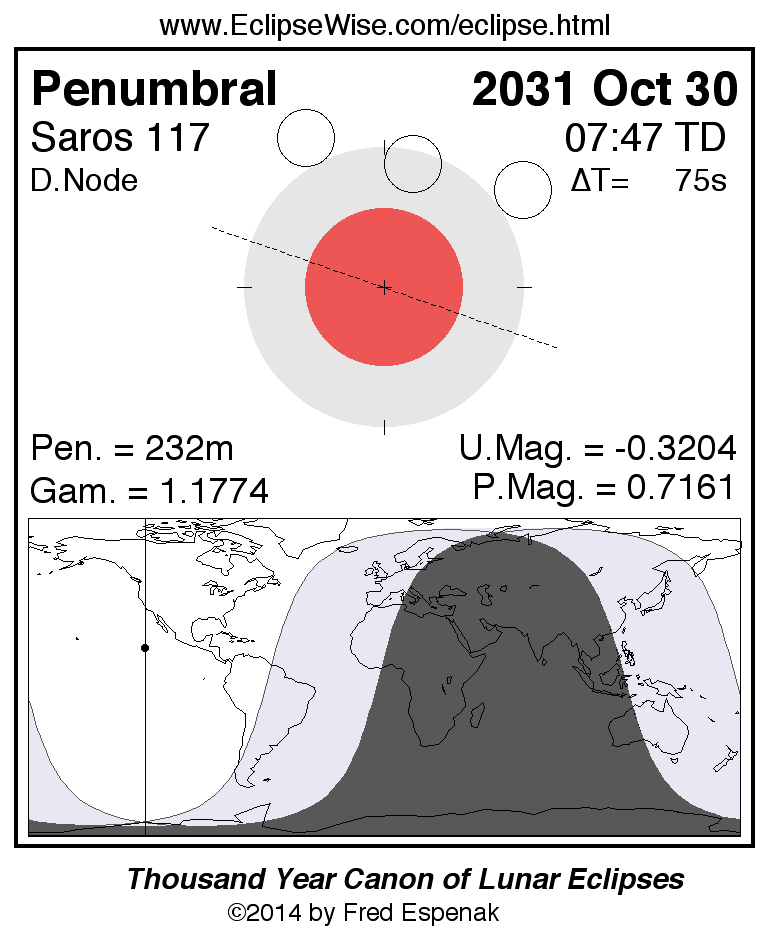
Penumbral Lunar Eclipse of 2031 Oct 30
Under Construction
Diagram and map of the eclipse (Figure 4).
Table 4 lists predicted umbral immersion and emersion times for 25 well-defined lunar craters. The timing of craters is useful in determining the atmospheric enlargement of Earth's shadow (see Crater Timings During Lunar Eclipses).
This is the xx th eclipse of Saros [6] series 117
Complete details for the xx eclipses in the series may be found at Saros 117.
For more information about this eclipse, see the EclipseWise Prime Page at Penumbral Lunar Eclipse of 2031 Oct 30
Click for larger more detailed figure
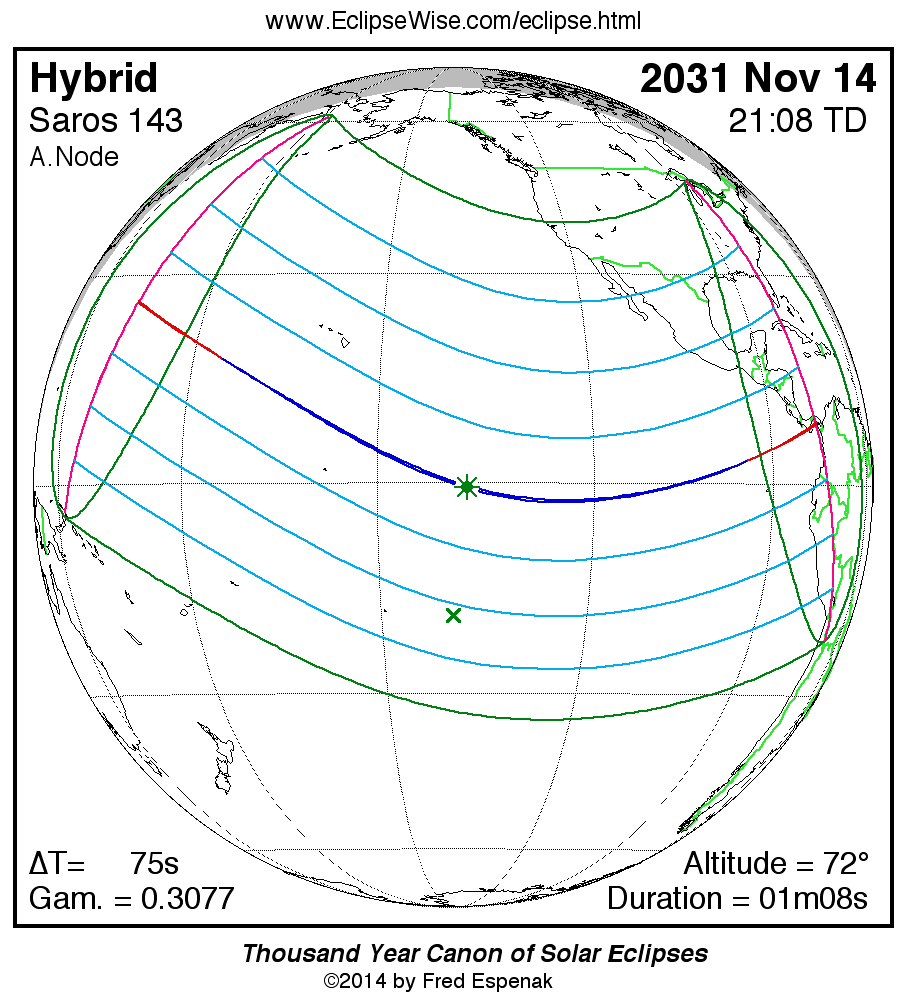
Hybrid Solar Eclipse of 2031 Nov 14
Under Construction
Map of the eclipse (Figure 5).
Local circumstances for a number of cities are given in Table 5.
The 2031 Nov 14 Solar Eclipse Circumstances Calculator is an interactive web page that can quickly calculate the local circumstances for the eclipse from any geographic location not included in the table.
The path of the eclipse is plotted on an interactive map at Google Map of the 2031 Nov 14 Solar Eclipse . This map permits zooming and scrolling as desired. Clicking the cursor on any location calculates the eclipse circumstances for that location. For more information see Key to Google Eclipse Maps.
This is the xx th eclipse of Saros [6] series 143.
Complete details for the xx eclipses in the series may be found at Saros 143.
For more information about this eclipse, see the EclipseWise Prime Page at Hybrid Solar Eclipse of 2031 Nov 14.
Explanatory Information
Solar Eclipse Figures
Lunar Eclipse Figures
Enlargement of Earth's Shadows and Lunar Eclipses
Danjon Scale of Lunar Eclipse Brightness
Moon's Apparent Magnitude During Total Lunar Eclipses
Crater Timings During Lunar Eclipses
Eclipse Altitudes and Azimuths
The altitude a and azimuth A of the Sun or Moon during an eclipse depend on the time and the observer's geographic coordinates. They are calculated as follows:
h = 15 (GST + UT - α ) + λ
a = arcsin [sin δ sin φ + cos δ cos h cos φ]
A = arctan [-(cos δ sin h)/(sin δ cos φ - cos δ cos h sin φ)]
where
h = hour angle of Sun or Moon
a = altitude
A = azimuth
GST = Greenwich Sidereal Time at 0:00 UT
UT = Universal Time
α = right ascension of Sun or Moon
δ = declination of Sun or Moon
λ = observer's longitude (east +, west -)
φ = observer's latitude (north +, south -)
During the eclipses of 2031 , the values for GST and the geocentric Right Ascension and Declination of the Sun or the Moon (at greatest eclipse) are as follows:
Eclipse Date GST α δ
Penumbral Lunar 2031 May 07 14.987 14.916 -17.791
Annular Solar 2031 May 21 15.916 3.860 20.161
Penumbral Lunar 2031 Jun 05 16.914 16.891 -21.054
Penumbral Lunar 2031 Oct 30 2.562 2.272 14.831
Hybrid Solar 2031 Nov 14 3.585 15.325 -18.337
Two web based tools that can also be used to calculate the local circumstances for all solar and lunar eclipses visible from any location. They are the Javascript Solar Eclipse Explorer and the Javascript Lunar Eclipse Explorer. The URLs for these tools are:
Javascript Solar Eclipse Explorer: www.EclipseWise.com/solar/JSEX/JSEX-index.html
Javascript Lunar Eclipse Explorer: www.EclipseWise.com/lunar/JLEX/JLEX-index.html
Eclipses During 2032
In 2032, there are 2 solar eclipses and 2 lunar eclipses:
| Eclipses During 2032 | |||
| 2032 Apr 25: Total Lunar Eclipse | |||
| 2032 May 09: Annular Solar Eclipse | |||
| 2032 Oct 18: Total Lunar Eclipse | |||
| 2032 Nov 03: Partial Solar Eclipse | |||
| Eclipses During 2032 | |||
|
Total Lunar Eclipse 2032 Apr 25 
|
Annular Solar Eclipse 2032 May 09 
|
Total Lunar Eclipse 2032 Oct 18 
|
Partial Solar Eclipse 2032 Nov 03 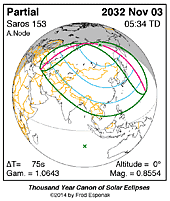
|
A full report Eclipses During 2032 will be published in Observer's Handbook:2032
Eclipse Web Sites
EclipseWise.com is a website dedicated to predictions and information on eclipses of the Sun and Moon. It offers a graphically intuitive interface and contains maps, diagrams, tables, and information about every solar and lunar eclipse from 2000 BCE to 3000 CE. This period includes 11898 solar eclipses and 12064 lunar eclipses.
Much of EclipseWise.com is based on the Thousand Year Canon of Solar Eclipses 1501 to 2500 (Espenak 2014a) and the Thousand Year Canon of Lunar Eclipses 1501 to 2500 (Espenak 2014b). These eclipse predictions use the Jet Propulsion Lab's DE406 — a computer ephemeris used for calculating high precision coordinates of the Sun and Moon for thousands of years into the past and future.
For eclipses over a larger time interval see Five Millennium Canon of Solar Eclipses –1999 to +3000 and Five Millennium Canon of Lunar Eclipses –-1999 to +3000.
The World Atlas of Solar Eclipses provides maps of all central eclipse paths from 2000 BCE to 3000 CE.
MrEclipse.com targets solar and lunar eclipse photography, with tips on eclipse observing and eye safety.
Eclipse Publications

|

|

|

|

|

|
Acknowledgments
All eclipse predictions were generated on a Macintosh G4 PowerPC using algorithms developed from the Explanatory Supplement [1974] with additional algorithms from Meeus, Grosjean, and Vanderleen [1966]. The solar and lunar coordinates used in the eclipse predictions are based on the JPL DE405. The difference between Terrestrial Time (TT) and Coordinated Universal Time (UTC) used in these predictions is 69.184 seconds (= 32.184 seconds plus 37 leap seconds).
For lunar eclipses, the elliptical shape of the umbral and penumbral shadows were calculated using Herald and Sinnott (2014) method of enlarging Earth's radius to compensate for the opacity of the terrestrial atmosphere (including corrections for the oblateness of Earth).
All calculations, diagrams, tables, and opinions presented in this paper are those of the author, and he assumes full responsibility for their accuracy.
Permission is granted to reproduce the eclipse data when accompanied by a link to this page and an acknowledgment:
"Eclipse Predictions by Fred Espenak, EclipseWise.com"
The use of diagrams and maps is permitted provided that they are unaltered (except for re-sizing) and the embedded credit line is not removed or covered.
Footnotes
[1] UTC or Coordinated Universal Time is the primary time standard that regulates world clocks and time. It is based on International Atomic Time (TAI) with leap seconds added at irregular intervals to compensate for the slowing of Earth's rotation. Leap seconds keep UTC within 0.9 second of UT1 (UT1 is mean solar time at 0° longitude). UTC is not adjusted for daylight saving time. It is effectively a successor to Greenwich Mean Time (GMT).
[2] The instant of greatest eclipse for solar eclipses occurs when the distance between the Moon's shadow axis and Earth's geocenter reaches a minimum.
[3] Eclipse magnitude for solar eclipses is defined as the fraction of the Sun's diameter occulted by the Moon.
[4] Eclipse obscuration is defined as the fraction of the Sun's area occulted by the Moon.
[5] For solar eclipses, gamma is the distance of the Moon's shadow axis from Earth's center (in Earth radii) when it reaches its minimum absolute value.
[6] The Saros is a period of 6,585.3 days (18 years 11 days 8 hours) in which eclipses (both solar and lunar) repeat. The geometry isn't exact but close enough for a Saros series to last 12 or more centuries.
[7] The instant of greatest eclipse for lunar eclipses occurs when the distance between the Moon and Earth's shadow axis reaches a minimum.
[8] Umbral eclipse magnitude is defined as the fraction of the Moon's diameter occulted by Earth's umbral shadow.
[9] For lunar eclipses, gamma is the distance of the Moon's center from Earth's shadow axis (in Earth radii) when it reaches its minimum absolute value.
[10] Penumbral eclipse magnitude is defined as the fraction of the Moon's diameter occulted by Earth's penumbral shadow.
References
Chauvenet, W., Manual of Spherical and Practical Astronomy, Vol.1, 1891 (Dover edition 1961).
Danjon, A., "Les éclipses de Lune par la pénombre en 1951," L'Astronomie, 65, 51-53 (Feb. 1951).
Espenak, F., Meeus, J., Five Millennium Canon of Solar Eclipses –1999 to +3000, 2nd Edition, AstroPixels Publishing, Portal, AZ, 2021.
Espenak, F., Meeus, J., Five Millennium Canon of Lunar Eclipses –-1999 to +3000, 2nd Edition, AstroPixels Publishing, Portal, AZ, 2021.
Espenak, F., Thousand Year Canon of Solar Eclipses 1501 to 2500, AstroPixels Publishing, Portal, AZ, 2014.
Espenak, F., Thousand Year Canon of Lunar Eclipses 1501 to 2500, AstroPixels Publishing, Portal, AZ, 2014.
Espenak, F., 21st Century Canon of Solar Eclipses, AstroPixels Publishing, Portal, AZ, 2016.
Espenak, F., 21st Century Canon of Lunar Eclipses, AstroPixels Publishing, Portal, AZ, 2020.
Espenak, F., Atlas of Central Solar Eclipses in the USA, AstroPixels Publishing, Portal, AZ, 2016.
Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, Her Majesty's Nautical Almanac Office, London, 1974.
Herald, D., and Sinnott, R. W., “Analysis of Lunar Crater Timings, 1842–2011,” J. Br. Astron. Assoc., 124, 5, 2014.
Hire P. de la, Tabulae Astronomicae, Paris, 1687.
Keen, R. A., "Volcanic Aerosols and Lunar Eclipses", Science, vol. 222, p. 1011-1013, Dec. 2, 1983.
Meeus, J., Elements of Solar Eclipses 1951-2200, Willmann-Bell, Richmond, VA (1989).






