Eclipses During 2024
By Fred Espenak
Based on the Article Published in
Observer's Handbook
2024
,
Royal Astronomical Society of Canada
In 2024, there are 2 solar eclipses and 2 lunar eclipses:
| Eclipses During 2024 | |||
| 2024 Mar 25: Penumbral Lunar Eclipse | |||
| 2024 Apr 08: Total Solar Eclipse | |||
| 2024 Sep 18: Partial Lunar Eclipse | |||
| 2024 Oct 02: Annular Solar Eclipse | |||
| Eclipses During 2024 | |||
|
Penumbral Lunar Eclipse 2024 Mar 25 
|
Total Solar Eclipse 2024 Apr 08 
|
Partial Lunar Eclipse 2024 Sep 18 
|
Annular Solar Eclipse 2024 Oct 02 
|
Unless otherwise stated, all times and dates used in this publication are in Universal Time or UT1 [1]. This astronomically derived time system is colloquially referred to as Greenwich Mean Time or GMT. To learn more about UT1 and how to convert UT1 to your own local time, see Time Zones and Universal Time.
Click for larger more detailed figure
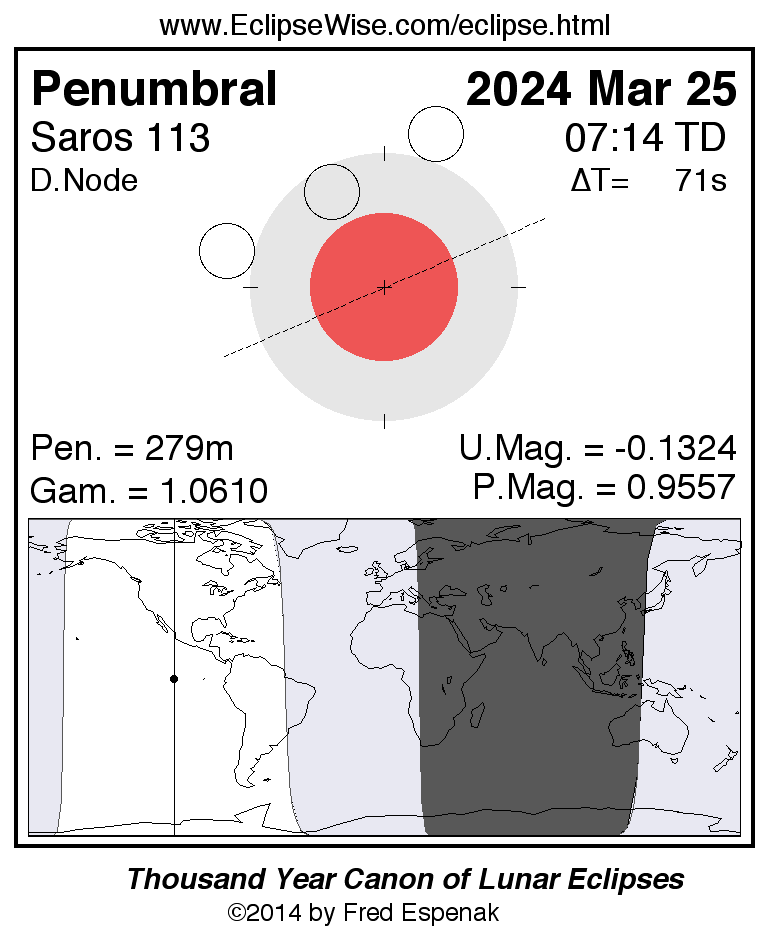
Penumbral Lunar Eclipse of 2024 Mar 25
The first eclipse of the year is a penumbral lunar eclipse occurring at the lunar orbit’s descending node in Virgo. This is a very deep penumbral eclipse with a penumbral magnitude [10]of 0.9577 and an eclipse duration of 279.9 minutes.
The Moon passes through the northern part of Earth’s penumbral shadow as shown in Figure 1. The times of the major eclipse phases are as follows.
Penumbral Eclipse Begins: 04:53:09 UTC
Greatest Eclipse: 07:12:51 UTC
Penumbral Eclipse Ends: 09:33:01 UTC
The beginning and end of a penumbral eclipse are not visible to the naked eye. In fact, no shading can be detected until about 2/3 of the Moon’s disk is immersed in the penumbra. This would correspond to about 06:25 UTC when the penumbral eclipse is first detectable. Keep in mind that this is only an estimate. Atmospheric conditions and the observer’s visual acuity are important factors to consider. An interesting exercise is to note when penumbral shading is first and last detected with the naked eye or binoculars.
At the instant of greatest eclipse [7] (07:12:51 UTC), the Moon lies at the zenith for a point in the Pacific Ocean about 800 kilometers west of the Galapagos Islands. The entire event is visible from most of North America and South America, and the Pacific Ocean. None of the eclipse will be visible from eastern Europe, eastern Africa, Asia, and western Australia.
The March 25 eclipse is the 64th eclipse of Saros series 113. The series is composed of 71 lunar eclipses in the following sequence: 7 penumbral, 23 partial, 13 total, 18 partial, 10 penumbral eclipses (Espenak and Meeus, 2021b). Saros 113 spans 1262.1 years and runs from the years 888 to 2150.
Complete details for the 71 eclipses in the series may be found at Saros 113.
For more information about this eclipse, see the EclipseWise Prime Page at Penumbral Lunar Eclipse of 2024 Mar 25.
Click for larger more detailed figure
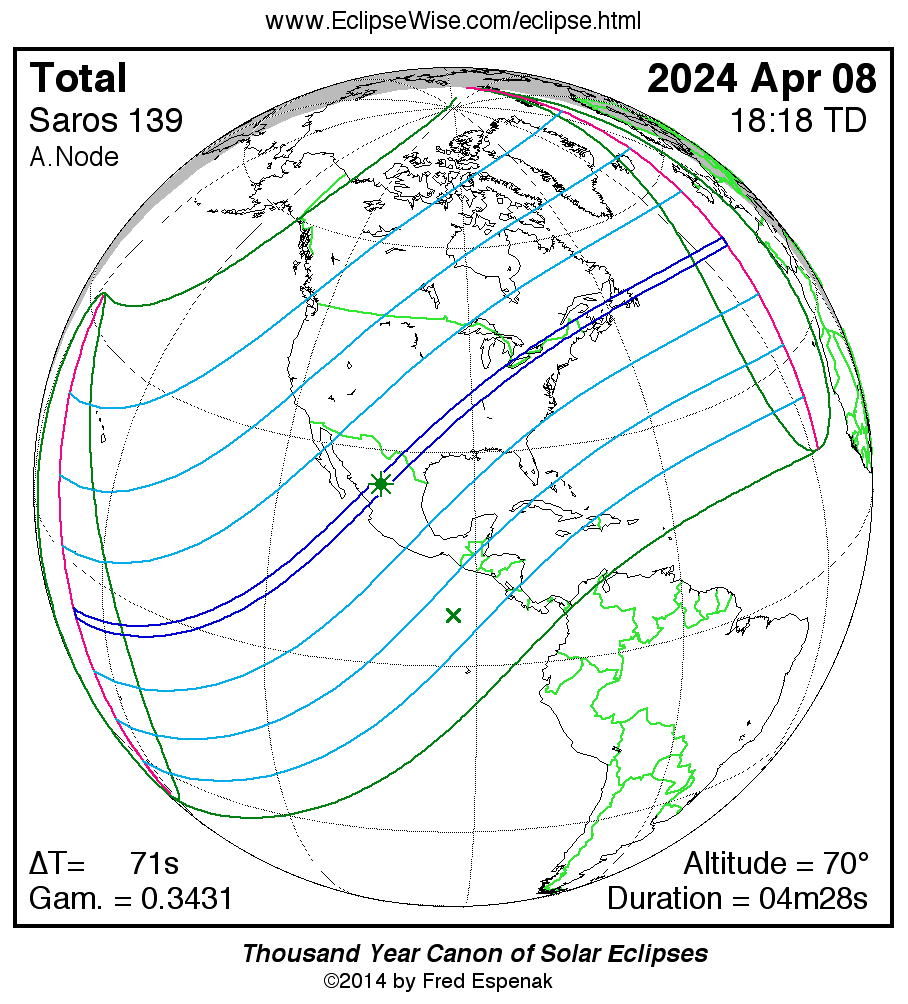
Total Solar Eclipse of 2024 Apr 08
The most anticipated event of 2024 is the total solar eclipse of April 08. Totality, the total phase of the eclipse, will be visible from within a 142– to 202–kilometer-wide corridor, which traverses North America (Figure 2). The Moon’s umbral shadow crosses northern Mexico before reaching the USA. Traveling southwest to northeast, it sweeps through parts of fifteen states: Texas, Oklahoma, Arkansas, Missouri, Tennessee, Kentucky, Illinois, Indiana, Ohio, Michigan, Pennsylvania, New York, Vermont, New Hampshire, and Maine. The path of totality also crosses six Canadian provinces: Ontario, Québec, New Brunswick, Prince Edward Island, Nova Scotia, and Newfoundland. The Moon’s penumbral shadow produces a partial eclipse visible from a much larger region covering most of North America.
The path of totality begins at 16:40 UTC in the South Pacific. No major landfall occurs during the first 85 min of the central eclipse as the Moon’s shadow sweeps northeast.
The track first encounters land among Mexico’s Islas Marias at 18:05 UTC (11:05 MST). Five minutes later (18:10 UTC; 11:10 MST), the umbra reaches Mexico’s Pacific coast near Mazatlán. The central-line duration of totality is 4 min 27 s and the Sun stands 69° above the horizon. The path width is 199 km as the shadow pursues its eastward track with a ground velocity of 0.70 km/s (1566 mph).
The path climbs the Sierra Madre Occidental mountains and enters the Mexican Plateau consisting of desert plains and low mountain ridges. It is here that the umbra reaches the point of greatest eclipse [2] at 18:17:20 UTC (12:17:20 CST). The duration of totality is 4 min 28 s and the Sun’s altitude is 70°.
Climbing over the Sierra Madre Oriental, the lunar shadow descends into the lowlands of the Gulf Coastal Plains, reaching the Rio Grande River.
The track enters Texas at 18:30 UTC (13:30 CDT) where the central duration is 4 min 27 s. Among the larger Texan cities in the path are: San Antonio (on the southern limit), Austin (1 min 43 s), Waco (4 min 12 s), Dallas (3 min 51 s), Fort Worth (2 min 32 s), and Texarkana (2 min 22 s). Figure 3 illustrates the path of totality through Mexico and the southern USA.
The lunar shadow cuts across the southeastern corner of Oklahoma and enters Arkansas (Little Rock, duration 2 min 26 s). The southeastern corner of Missouri also falls within the totality track. Cape Girardeau is Missouri’s largest city in the path and gets 4 min 6 s of totality. Carbondale, Illinois, experiences its second total solar eclipse in 6 3/4 years.
Southern Indiana stands in the umbra’s path (Indianapolis: 3 min 48 s). The path narrowly misses several large cities nearby including Memphis, Tennessee (mag=0.976), St. Louis, Missouri (mag=0.987), and Louisville, Kentucky (mag=0.989).
The shadow’s trajectory takes it through Ohio, northwestern Pennsylvania (Erie: 3 min 42 sec), and New York (Buffalo: 3 min 45 s).
In Canada (Figure 4), the northern edge of the path crosses into Ontario (Hamilton: 1 min 43 s). Unfortunately, Toronto lies 9 km outside the path thereby missing totality with a magnitude 0.997 partial eclipse. Downtown Québec City experiences 1 min 27 s of totality.
Back in the USA (Figure 4), the path crosses Vermont (Burlington: 3 min 14 s), New Hampshire and Maine, before leaving the country to enter Canada exclusively in New Brunswick (Fredericton: 2 min 14 s). Western Prince Edward Island lies in the path, but Charlottetown is outside, where a partial eclipse of magnitude 0.992 occurs. The shadow track also clips northern Nova Scotia.
Crossing the Gulf of St. Lawrence, Québec’s Magdalen Islands straddle the central line. The last landfall of the umbral shadow is in southern Newfoundland. The late afternoon Sun is just 24° above the horizon and the central-line duration is 2 min 54 s.
Leaving Canada with a velocity of 2.08 km/s (4650 mph), the umbra races 2450 km across the North Atlantic Ocean before reaching the end of the track and returning to space. Over a period of 3 h 15 min, the umbra travels along a 14,800 km (9200 miles) track that covers an over 0.52% of Earth’s surface. Path coordinates and central-line circumstances are presented in Table 1.
Local circumstances for cities in Canada given in Table 2 (Canada - Total), Table 3 (Canada 1 - Partial), and Table 4 (Canada 2 - Partial). All times are provided in Local Time (including Daylight Saving Time). The Sun’s altitude and azimuth, the eclipse magnitude [3], and obscuration [4], are all listed for the instant of maximum eclipse.
Local circumstances for cities in the USA and Mexico given in Table 5 (USA - Total), Table 6 (USA - Partial), and Table 7 (Mexico - Total). All times are provided in Local Time (including Daylight Saving Time). The Sun’s altitude and azimuth, the eclipse magnitude [3], and obscuration [4], are all listed for the instant of maximum eclipse.
The 2024 Apr 08 Solar Eclipse Circumstances Calculator is an interactive web page that can quickly calculate the local circumstances for the eclipse from any geographic location not included in Tables 2 through 7.
The path of the eclipse is plotted on an interactive map at Google Map of the 2024 Apr 08 Solar Eclipse . This map permits zooming and scrolling as desired. Clicking the cursor on any location calculates the eclipse circumstances for that location. For more information see Key to Google Eclipse Maps.
This is the 30th eclipse of Saros [6] series 139, a middle-aged series, which produced its first central eclipse (hybrid) on 1627 Aug. 11. The next 11 eclipses were all hybrid eclipses until the first of a string 43 total eclipses began on 1843 Dec. 21. Following 2024, the next eclipse in the series will be on 2042 Apr. 20. The entire series is composed of 71 solar eclipses in the following sequence: 7 partial, 12 hybrid, 43 total, and 9 partial eclipses (Espenak and Meeus, 2021a). Saros series 139 runs from the years 1501 to 2763.
Complete details for the 71 eclipses in the series may be found at Saros 139.
For more information about this eclipse, see the EclipseWise Prime Page at Total Solar Eclipse of 2024 Apr 08.

|

|
Click for larger more detailed figure
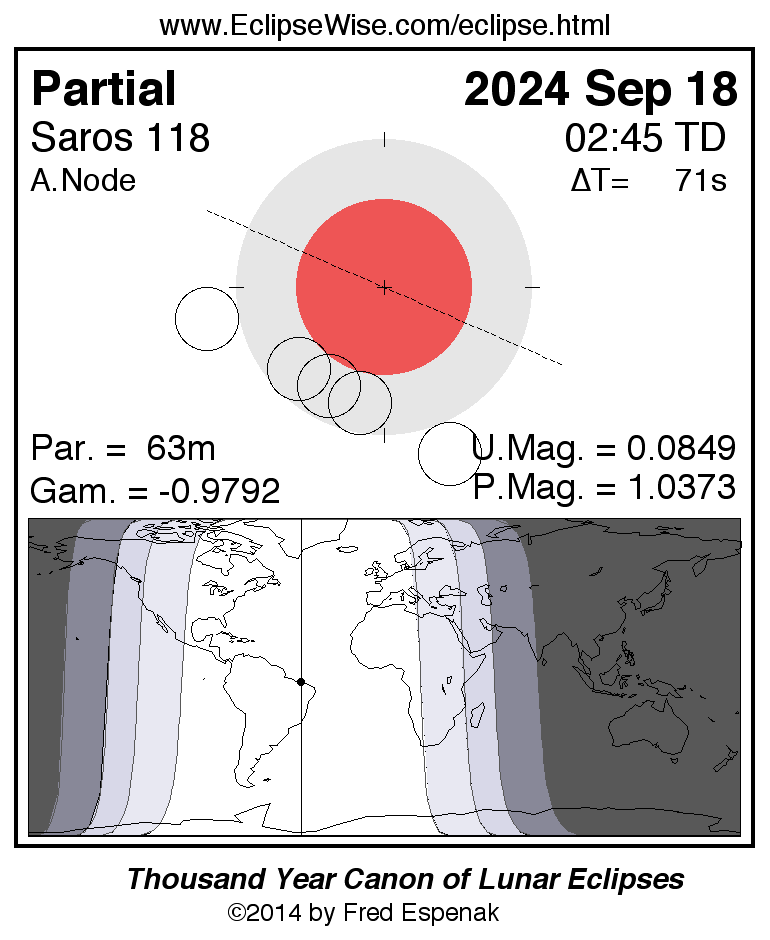
Partial Lunar Eclipse of 2024 Sep 18
The third eclipse of the year is a partial lunar eclipse. Once again, the event is well placed for the Western Hemisphere. The eclipse occurs at the ascending node of the Moon’s orbit in Pisces. Occurring 0.4 days before perigee (Sep. 18 at 13:28 UTC), the Moon will appear 31.8' in diameter. This is a relatively shallow partial eclipse with an umbral eclipse magnitude of 0.0869. At mid-eclipse the Moon’s northern limb dips just 3.1' into the umbral shadow.
The Moon’s path through Earth’s shadows and a map illustrating worldwide visibility of the event are shown in Figure 5. The times of the major eclipse phases are listed as follows.
Penumbral Eclipse Begins: 00:41:00 UTC
Partial Eclipse Begins: 02:12:45 UTC
Greatest Eclipse: 02:44:16 UTC
Partial Eclipse Ends: 03:16:24 UTC
Penumbral Eclipse Ends: 04:47:56 UTC
The instant of greatest eclipse (02:44:16 UTC) occurs with the Moon in the zenith for a point in northern Brazil near Sao Luis. This eclipse is visible from most of North and South America, Europe, and Africa. None of the eclipse is visible from Asia and Australia.
The Sep. 18 eclipse is the 52nd eclipse of Saros 118. This series is composed of 73 lunar eclipses in the following sequence: 9 penumbral, 7 partial, 28 total, 8 partial, 21 penumbral eclipses (Espenak and Meeus, 2021b). Saros 118 spans 1298.2 years and runs from 1105 to 2403.
For more information about this eclipse, see the EclipseWise Prime Page at Partial Lunar Eclipse of 2024 Sep 18
Click for larger more detailed figure
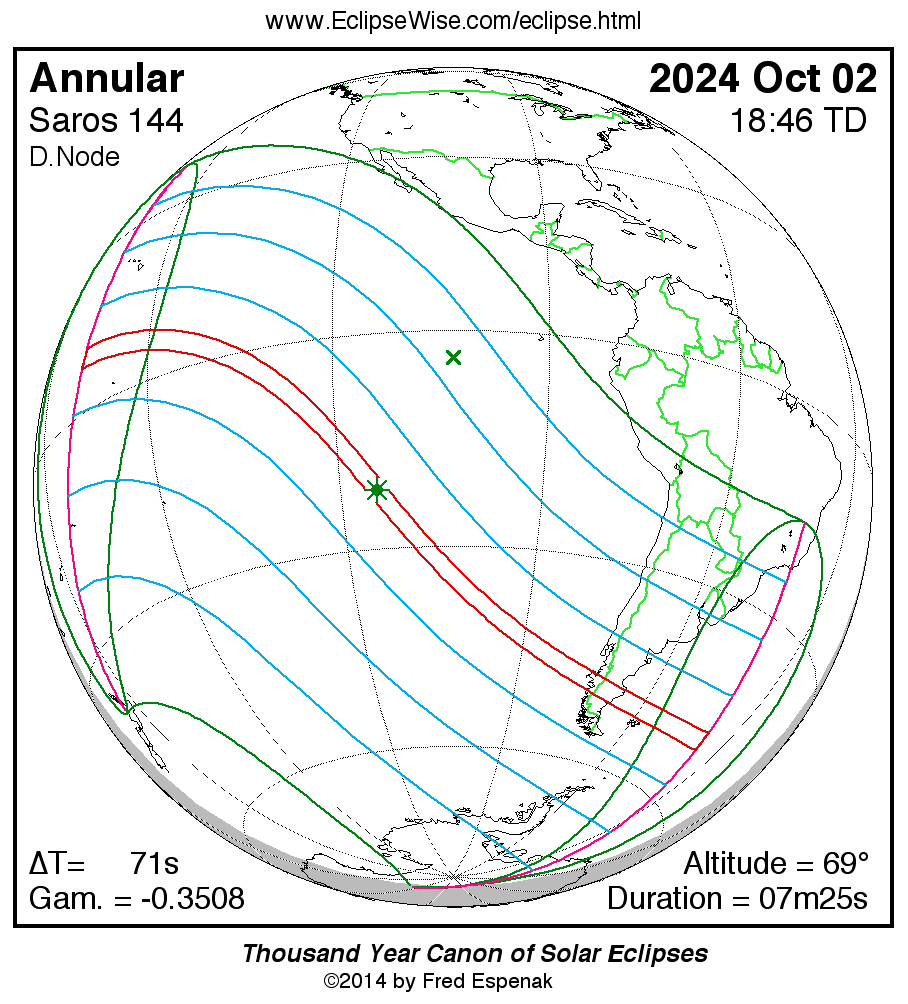
Annular Solar Eclipse of 2024 Oct 02
The second solar eclipse of 2024 is visible from the Western Hemisphere. Unfortunately, most of the annular eclipse track is over the Pacific Ocean (Figure 6).
The path of the annular eclipse begins in the central Pacific about 1700 kilometers southwest of the Hawaiian Islands at 16:54 UTC. It is there that the Moon’s antumbral shadow meets Earth and forms a 331-kilometer-wide corridor. The duration of the annular phase at sunrise is 5 min 39 s. Traveling southeast, the antumbra encounters no land over the first half of its trajectory.
The instant of greatest eclipse occurs at 18:45:04 UTC with a duration of annularity of 7 min 25 sec, a path width of 266 kilometers, and a Sun altitude of 69°. The eclipse magnitude is 0.933 and the eclipse obscuration is 0.870.
Twenty-two minutes later (19:07:15 UTC), first landfall occurs at Rapa Nui (aka Easter Island). The remote island is 68 kilometers northeast of the central line but the inhabitants there still experience 6 min 23 s of annularity.
Continuing its track through the South Pacific, the next landfall is along Chile’s rugged Patagonian coast more than an hour later at 20:22 UTC (Figure 7). The central line duration is 6 min 26 s and the Sun stands 27° above the western horizon. Crossing the southern Andes, the antumbra reaches Argentina at 20:24 UTC. In just 3 1/3 min, the shadow crosses the nation and reaches the South Atlantic coast at 20:27 UTC.
Passing north of the Falkland Islands, the antumbral path ends 550 kilometers north of South Georgia at 20:36 UTC.
Over the course of 3 h and 43 min, the Moon’s antumbral shadow traverses a 14 200-kilometer-long track covering 0.82% of Earth’s surface area.
The 2024 Oct 02 Solar Eclipse Circumstances Calculator is an interactive web page that can quickly calculate the local circumstances for the eclipse from any geographic location.
The path of the eclipse is plotted on an interactive map at Google Map of the 2024 Oct 02 Solar Eclipse . This map permits zooming and scrolling as desired. Clicking the cursor on any location calculates the eclipse circumstances for that location. For more information see Key to Google Eclipse Maps.
This is the 17th eclipse of Saros 144. The entire series is composed of 70 solar eclipses in the following sequence: 8 partial, 39 annular, and 23 partial eclipses (Espenak and Meeus, 2021a). Saros 144 lasts 1244.1 years running from 1736 to 2980. Complete details for the series may be found at Saros 144.
For more information about this eclipse, see the EclipseWise Prime Page at Annular Solar Eclipse of 2024 Oct 02.
Explanatory Information
Solar Eclipse Figures
Lunar Eclipse Figures
Enlargement of Earth's Shadows and Lunar Eclipses
Danjon Scale of Lunar Eclipse Brightness
Moon's Apparent Magnitude During Total Lunar Eclipses
Crater Timings During Lunar Eclipses
Eclipse Altitudes and Azimuths
The altitude a and azimuth A of the Sun or Moon during an eclipse depend on the time and the observer's geographic coordinates. They are calculated as follows:
h = 15 (GST + UT - α ) + λ
a = arcsin [sin δ sin φ + cos δ cos h cos φ]
A = arctan [-(cos δ sin h)/(sin δ cos φ - cos δ cos h sin φ)]
where
h = hour angle of Sun or Moon
a = altitude
A = azimuth
GST = Greenwich Sidereal Time at 0:00 UT
UT = Universal Time
α = right ascension of Sun or Moon
δ = declination of Sun or Moon
λ = observer's longitude (east +, west -)
φ = observer's latitude (north +, south -)
During the eclipses of 2024 , the values for GST and the geocentric Right Ascension and Declination of the Sun or the Moon (at greatest eclipse) are as follows:
Eclipse Date GST α δ
Penumbral Lunar Mar. 25 12.216 12.345 –1.202
Total Solar Apr. 08 13.166 1.194 7.591
Partial Lunar Sep. 18 23.835 23.768 –2.591
Annular Solar Oct. 02 0.798 12.616 –3.984
Two web based tools that can also be used to calculate the local circumstances for all solar and lunar eclipses visible from any location. They are the Javascript Solar Eclipse Explorer and the Javascript Lunar Eclipse Explorer. The URLs for these tools are:
Javascript Solar Eclipse Explorer: www.EclipseWise.com/solar/JSEX/JSEX-index.html
Javascript Lunar Eclipse Explorer: www.EclipseWise.com/lunar/JLEX/JLEX-index.html
Eclipses During 2025
In 2025, there are 2 solar eclipses and 2 lunar eclipses:
| Eclipses During 2025 | |||
| 2025 Mar 14: Total Lunar Eclipse | |||
| 2025 Mar 29: Partial Solar Eclipse | |||
| 2025 Sep 07: Total Lunar Eclipse | |||
| 2025 Sep 21: Partial Solar Eclipse | |||
| Eclipses During 2025 | |||
|
Total Lunar Eclipse 2025 Mar 14 
|
Partial Solar Eclipse 2025 Mar 29 
|
Total Lunar Eclipse 2025 Sep 07 
|
Partial Solar Eclipse 2025 Sep 21 
|
A full report Eclipses During 2025 will be published in Observer's Handbook:2025
Eclipse Web Sites
EclipseWise.com is a website dedicated to predictions and information on eclipses of the Sun and Moon. It offers a graphically intuitive interface and contains maps, diagrams, tables, and information about every solar and lunar eclipse from 2000 BCE to 3000 CE. This period includes 11898 solar eclipses and 12064 lunar eclipses.
Much of EclipseWise.com is based on the Thousand Year Canon of Solar Eclipses 1501 to 2500 (Espenak 2014a) and the Thousand Year Canon of Lunar Eclipses 1501 to 2500 (Espenak 2014b). These eclipse predictions use the Jet Propulsion Lab's DE406 — a computer ephemeris used for calculating high precision coordinates of the Sun and Moon for thousands of years into the past and future.
For eclipses over a larger time interval see Five Millennium Canon of Solar Eclipses –1999 to +3000 and Five Millennium Canon of Lunar Eclipses –-1999 to +3000.
The World Atlas of Solar Eclipses provides maps of all central eclipse paths from 2000 BCE to 3000 CE.
MrEclipse.com targets solar and lunar eclipse photography, with tips on eclipse observing and eye safety.
Acknowledgments
All eclipse predictions were generated on a Macintosh G4 PowerPC using algorithms developed from the Explanatory Supplement [1974] with additional algorithms from Meeus, Grosjean, and Vanderleen [1966]. The solar and lunar coordinates used in the eclipse predictions are based on the JPL DE405. For lunar eclipses, the elliptical shape of the umbral and penumbral shadows were calculated using Herald and Sinnott (2014) method of enlarging Earth's radius to compensate for the opacity of the terrestrial atmosphere (including corrections for the oblateness of Earth).
All calculations, diagrams, tables, and opinions presented in this paper are those of the author, and he assumes full responsibility for their accuracy.
Permission is granted to reproduce the eclipse data when accompanied by a link to this page and an acknowledgment:
"Eclipse Predictions by Fred Espenak, EclipseWise.com"
The use of diagrams and maps is permitted provided that they are unaltered (except for re-sizing) and the embedded credit line is not removed or covered.
Footnotes
[1] UT1 or Universal Time is the mean solar time on the Prime Meridian at Greenwich, England. Civil time signals are transmitted according to Coordinated Universal Time (UTC), which is based on International Atomic Time (TAI) with leap seconds added at irregular intervals to compensate for the slowing of Earth's rotation. The leap seconds keep UTC within 0.9 second of UT1.
[2] The instant of greatest eclipse for solar eclipses occurs when the distance between the Moon's shadow axis and Earth's geocenter reaches a minimum.
[3] Eclipse magnitude for solar eclipses is defined as the fraction of the Sun's diameter occulted by the Moon.
[4] Eclipse obscuration is defined as the fraction of the Sun's area occulted by the Moon.
[5] For solar eclipses, gamma is the distance of the Moon's shadow axis from Earth's center (in Earth radii) when it reaches its minimum absolute value.
[6] The Saros is a period of 6,585.3 days (18 years 11 days 8 hours) in which eclipses (both solar and lunar) repeat. The geometry isn't exact but close enough for a Saros series to last 12 or more centuries.
[7] The instant of greatest eclipse for lunar eclipses occurs when the distance between the Moon and Earth's shadow axis reaches a minimum.
[8] Umbral eclipse magnitude is defined as the fraction of the Moon's diameter occulted by Earth's umbral shadow.
[9] For lunar eclipses, gamma is the distance of the Moon's center from Earth's shadow axis (in Earth radii) when it reaches its minimum absolute value.
[10] Penumbral eclipse magnitude is defined as the fraction of the Moon's diameter occulted by Earth's penumbral shadow.
References
Chauvenet, W., Manual of Spherical and Practical Astronomy, Vol.1, 1891 (Dover edition 1961).
Danjon, A., "Les éclipses de Lune par la pénombre en 1951," L'Astronomie, 65, 51-53 (Feb. 1951).
Espenak, F., Meeus, J., Five Millennium Canon of Solar Eclipses –1999 to +3000, 2nd Edition, AstroPixels Publishing, Portal, AZ, 2021.
Espenak, F., Meeus, J., Five Millennium Canon of Lunar Eclipses –-1999 to +3000, 2nd Edition, AstroPixels Publishing, Portal, AZ, 2021.
Espenak, F., Thousand Year Canon of Solar Eclipses 1501 to 2500, AstroPixels Publishing, Portal, AZ, 2014.
Espenak, F., Thousand Year Canon of Lunar Eclipses 1501 to 2500, AstroPixels Publishing, Portal, AZ, 2014.
Espenak, F., 21st Century Canon of Solar Eclipses, AstroPixels Publishing, Portal, AZ, 2016.
Espenak, F., 21st Century Canon of Lunar Eclipses, AstroPixels Publishing, Portal, AZ, 2020.
Espenak, F., Atlas of Central Solar Eclipses in the USA, AstroPixels Publishing, Portal, AZ, 2016.
Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, Her Majesty's Nautical Almanac Office, London, 1974.
Herald, D., and Sinnott, R. W., “Analysis of Lunar Crater Timings, 1842–2011,” J. Br. Astron. Assoc., 124, 5, 2014.
Keen, R. A., "Volcanic Aerosols and Lunar Eclipses", Science, vol. 222, p. 1011-1013, Dec. 2, 1983.
Meeus, J., Elements of Solar Eclipses 1951-2200, Willmann-Bell, Richmond, VA (1989).









